Sur la piste des maths avec Bruno Wirtz

Rencontre avec le mathématicien Bruno Wirtz par notre envoyé spécial David Commarmond à l’occasion de l’EVA Paris 2022. De Thalès et Pythagore au Big Data, le Pr. Bruno Wirtz nous fait découvrir une autre façon d’appréhender la mesure et l’abstraction.

Mesure de la pensée, pensée de la mesure
Entretien avec Bruno Wirtz

Bruno Wirtz, normalien et agrégé de mathématiques, est maître de conférences en mathématiques à l'Université de Bretagne occidentale (UBO) depuis plus de 20 ans. Au tournant des années 2000, il s’est lancé dans l’aventure entrepreneuriale. C’est ainsi qu’il est devenu cofondateur et conseiller scientifique de l'entreprise Tellus-Environment dans le cadre d’un projet évoluant dans le domaine environnemental. Il répond aux questions d'ArkéoTopia sur son activité et la relation qu’entretiennent les Français avec les mathématiques, notamment dans le champ scientifique.

Pouvez-vous en dire plus sur votre activité au sein de Tellus-Environment ?

Ma spécialité dans l'entreprise est la modélisation. Cela consiste à confronter différents concepts mathématiques à des problématiques non mathématiques. L’archéologie et la géophysique, par le biais de rencontres, sont devenues pour moi un nouveau champ d’investigation et d’expérimentation.

Les derniers classements internationaux positionnent les élèves français parmi les plus faibles en mathématiques. Ce déficit de culture mathématique fait-il aussi défaut aux décideurs ? Comment s’organise ce dialogue quand l’autre ne parle pas le langage des mathématiques ?

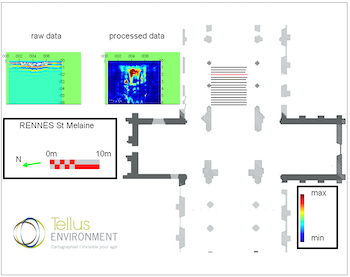Cette question est cruciale pour la discipline. C'est la raison pour laquelle je parle de mathématiques du réel, et non de mathématiques appliquées. Il s'agit de construire, pour chaque problème posé, un assemblage de concepts mathématiques pour élaborer une solution. Tout comme une démonstration mathématique consistante, il s'agit de bâtir un synopsis, donc une durée.

Ce concept va à rebours de l'instantané, du temps consommé par notre présent, au niveau du grand public. Celui-ci est souvent intéressé par le résultat directement visible, non par la démarche intellectuelle. Cette démarche devient intéressante aux yeux du plus grand nombre quand elle produit un résultat.

Les professionnels auxquels je suis confronté sont de deux sortes :

1. les utilisateurs simples de capteurs, souvent issus du monde militaire,
2. des cadres ayant une formation scientifique plus poussée.

Les premiers consomment sans état d'âme mais avec confiance les résultats produits par mes procédés. Les seconds sont souvent très réservés car ces inventions de rupture remettent en cause leurs pratiques, leur culture scientifique, leurs compétences. Là se trouvent les freins à l'innovation.

Les décideurs restent perplexes car ils sentent une contradiction entre des experts à l'ancienne qui sont critiques vis-à-vis de nos travaux et les résultats probants que nous obtenons sur le terrain. Ils appellent Tellus-Environment surtout pour des cas difficiles et urgents qui ont tenu en échec les spécialistes traditionnels. Pour la décision politique, les cinq dernières années ont apporté un vent plus favorable à l'innovation qu'auparavant.

Le dialogue avec les non-mathématiciens est possible, d'autant plus efficace que l'interlocuteur se croit loin des mathématiques. Mais c'est un jeu de billard. Les concepts les plus abstraits pénètrent l'esprit de l'autre par la bande, par la « pitite question » façon Homer Simpson. J'ai enseigné quelques années les mathématiques générales et les probabilités/statistiques aux archéologues de l'INRAP. Ils avaient la consigne d'apporter leurs propres données sous format numérique. J'en ai traité en direct pendant mon cours. Plusieurs fois, les archéologues ont compris, par mon entremise, l'information importante écrite en filigrane dans leur data. Leur sourire et l'éclat de leur regard à ce moment restent gravés dans ma mémoire.

Est-il possible d’améliorer son niveau en mathématiques tout au long de sa vie ? Pourquoi est-ce si peu valorisé dans la formation continue ?

Il est toujours possible d'améliorer son niveau mathématique. La difficulté est de trouver la motivation pour le faire. L'essence de cette motivation est la curiosité : sa capacité à retrouver un regard d'enfant en observant le monde. Malheureusement, nous avons plus souvent un regard de consommateur qu'un regard d'enfant.

La formation continue est vue comme une augmentation du savoir-faire plus que du savoir. Elle ne remet pas en cause les savoir fondamentaux des étudiants adultes. Elle s’intéresse à des portions très étroites d'une activité et s'adresse en général à un public déjà impliqué dans un secteur professionnel très précis. Aussi les mathématiques, par essence plus généralistes, sont peu présentes dans ce secteur.

Thalès et Pythagore ont-ils encore quelque chose à nous dire ?

Thalès a dit : tout est ombre. Pythagore a dit : tout est nombre. Pour mémoire, Thalès a mesuré la hauteur de la grande pyramide en mesurant la longueur de son ombre. Dans le triangle pythagoricien 3-4-5 le nombre 5 est un calcul, non une mesure. C'est donc de la pensée.

Dans notre monde foisonnent les data, c'est-à-dire des mesures. La puissance de calcul, dont l'intelligence artificielle est le dernier avatar, consomme la mesure avec la notion fondamentale de distance chère à Pythagore.

Sommairement, la mémoire est une collection de points. Une nouvelle information est donc un nouveau point proche d'un point déjà en mémoire. Les concepts derrière les mots mémoire et distance sont très riches et très élaborés, mais la notion de distance est en filiation directe avec celle de Pythagore.

La pensée chère à Pythagore est a priori absente de l'intelligence artificielle, mais bien présente dans celle de ses concepteurs. Si ce domaine est efficace dans certains domaines comme la reconnaissance faciale ou le diagnostic de certaines maladies, il en est d'autres qui semblent lui résister comme la reconnaissance automatique des objets manufacturés. Sur ces questions la pensée purement humaine reste d'actualité.

Comme pour la certification Voltaire, est-il envisageable d’imaginer une certification ou des certifications en mathématiques (Pythagore, Euclide, Pascal….) que chacun pourrait suivre tout au long de la vie ?

La mathématique si universelle relève plus que les autres disciplines de l'intime dans l'esprit de chaque individu. Quand je dis que je suis mathématicien, les gens réagissent souvent en disant qu'ils sont « nuls en maths » avec une épaisse chape de complexes. Ce genre de réaction existe beaucoup moins avec les autres disciplines. Aussi, une inscription à une certification qui est publique devrait souvent vaincre une douleur personnelle avec les mathématiques.

Pourrait-on rendre les mathématiques plus ludiques ?

De mes souvenirs d'enseignant, j'ai pu faire passer des concepts délicats en annihilant la peur de la discipline dans l'esprit des étudiants. Le jeu, l'image, la théâtralisation du cours, l'humour sont des armes contre la peur. La culture scientifique de l'enseignant représente une aide précieuse pour pénétrer les esprits.

Pour aller plus loin

• Découvrir la dimension archéologique de l'entreprise Tellus-Environment
• Mathématiques du réel : assemblage de différents concepts et savoirs mathématiques pour résoudre un problème non issu des mathématiques.

Vous souhaitez que nous fassions une interview, une critique de livre, de documentaire ou de support en relation avec l'archéologie, que ce soit pour le grand public, des enfants ou des spécialistes, n'hésitez pas à écrire à ArkéoTopia via notre formulaire.

ArkéoTopia, une autre voie pour l'archéologie® a vocation à porter un autre regard sur l’archéologie d’aujourd’hui pour mieux aider à préparer celle de demain. Pour en savoir plus sur l'association, n'hésitez pas à prendre connaissance de notre vidéo institutionnelle et de nos actions.